首页 -> 2002年第8期
美与物理学
作者:杨振宁
惊叹他的独创力,然而会觉得问题还没有做完,没有做干净,还要发展下去;而读了狄拉克的文章,你也会惊叹他的独创力,同时却觉得他似乎已把一切都发展到了尽头,没有什么再可以做下去了。
前面提到狄拉克的文章给人“秋水文章不染尘”的感受,海森堡的文章则完全不同,二者对比清浊分明。我想不到有什么诗句或成语可以描述海森堡的文章,既能道出他的天才的独创性,又能描述他的思路中不清楚、有渣滓、有时似乎茫然乱摸索的特点。
物理学与数学
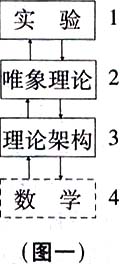
海森堡和狄拉克的风格为什么如此不同?主要原因是他们所专注的物理学内涵不同。为了解释此点,请看图一所表示的物理学的三个部门和其中的关系:唯象理论(2)是介乎实验(1)和理论架构(3)之间的研究。(1)和(2)合起来是实验物理,(2)和(3)合起来是理论物理,而理论物理的语言是数学。
物理学的发展通常自实验(1)开始,即自研究现象开始。关于这一发展过程,我们可以举很多大大小小的例子。这里举牛顿力学的历史为例。布拉赫是实验天体物理学家,活动领域是(1)。他做了关于行星轨道的精密观测。后来开普勒仔细分析布拉赫的数据,发现了有名的开普勒三大定律。这是唯象理论(2)。最后牛顿创建了牛顿力学与万有引力理论,其基础就是开普勒的三大定律。这是理论架构(3)。
海森堡和狄拉克的工作集中在图一所显示的哪一些领域呢?狄拉克最重要的贡献是前面所提到的狄拉克方程。海森堡最重要的贡献是海森堡方程,是量子力学的基础:
pq-qp=-ih (H)
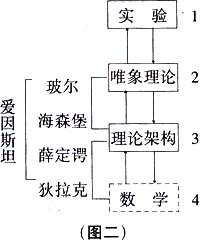
这两个方程都是理论架构(3)中之尖端贡献。二者都达到物理学的最高境界。可是写出这两个方程的途径却截然不同:海森堡的灵感来自他对实验结果(1)与唯象理论(2)的认识,进而在摸索中达到了方程式(H)。狄拉克的灵感来自他对数学(4)的美的直觉欣赏,进而天才地写出他的方程(D)。他们二人喜好的、注意的方向不同,所以他们工作的领域也不一样,如图二所示;(此图也标明玻尔、薛定谔和爱因斯坦的研究领域。爱因斯坦兴趣广泛,在许多领域中,自(2)至(3)至(4),都曾做出划时代的贡献。)
海森堡从实验(1)与唯象理论(2)出发:实验与唯象理论是五光十色,错综复杂的,所以他要摸索,要犹豫,要尝试了再尝试,因此他的文章也就给读者不清楚、有渣滓的感觉。狄拉克则从他对数学的灵感出发:数学的最高境界是结构美,是简洁的逻辑美,因此他的文章也就给读者“秋水文章不染尘”的感受。
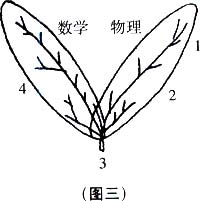
让我补充一点关于数学和物理的关系。我曾经把二者的关系表示为两片在茎处重叠的叶片(图三)。重叠的地方同时是二者之根、二者之源。譬如微分方程、偏微分方程、希尔伯特空间、黎曼几何和纤维丛等,今天都是二者共用的基本观念。这是惊人的事实,因为首先达到这些观念的物理学家与数学家曾遵循完全不同的路径、完全不同的传统。为什么会殊途同归呢?大家今天没有很好的答案,恐怕永远不会有,因为答案必须牵扯到宇宙观、知识论和宗教信仰等难题。
必须注意的是在重叠的地方,共同的基本观念虽然如此惊人地相同,但是重叠的地方并不多,只占二者各自的极少部分。譬如实验(1)与唯象理论(2)都不在重叠区,而绝大部分的数学工作也在重叠区之外。另外值得注意的是即使在重叠区,虽然基本观念物理与数学共用,但是二者的价值观与传统截然不同,而二者发展的生命力也各自遵循不同的茎脉流通,如图三所示。
常常有年轻朋友问我,他应该研究物理,还是研究数学。我的目答是这要看你对哪一个领域里的美和妙有更高的判断能力和更女的喜爱。爱因斯坦在晚年时曾经讨论过为什么他选择了物理。他说:
在数学领域里,我的直觉不够,不能辨认哪些是真正重要的研究,哪些只是不重要的题目。而在物理学领域里,我很快学到怎样找到基本问题来下功夫。
年轻人面对选择前途方向时,要对自己的喜好与判断能力有正确的自我估价。
美与物理学
物理学自(1)到(2)到(3)是自表面向深层的发展。表面有表面的结构,有表面的美。譬如虹和霓是极美的表面现象,人人都可以看到。实验工作者作了测量以后发现虹是42°的弧,红在外,紫在内;霓是50°的弧,红在内,紫在外。这种准确规律增加了实验工作者对自然现象的美的认识。这是第一步(1)。进一步的唯象理论研究(2)使物理学家了解到这42°与50°可以从阳光在水珠中的折射与反射推算出来,此种了解显示出了深一层的美。再进一步的研究更深入了解折射与反射现象本身可从一个包容万象的麦克斯韦方程推算出来,这就显示出了极深层的理论架构(3)的美。
牛顿的运动方程、麦克斯韦方程、爱因斯坦的狭义与广义相对论方程、狄拉克方程、海森堡方程和其他五六个方程是物理学理论架构的骨干。它们提炼了几个世纪的实验工作(1)与唯象理论(2)的精髓,达到了科学研究的最高境界。它们以极度浓缩的数学语言写出了物理世界的基本结构,可以说它们是造物者的不朽诗篇。
这些方程还有一方面与诗有共同点:它们的内涵往往随着物理学的发展而产生新的、当初所完全没有想到的意义。举两个例子:上面提到过的19世纪中叶写下来的麦克斯韦方程是在本世纪初通过爱因斯坦的工作才显示出高度的对称性,而这种对称性以后逐渐发展为20世纪物理学的一个最重要的中心思想。另一个例子是狄拉克方程。它最初完全没有被数学家所注意,而今天狄拉克流型已成为数学家研究的一个热门新课题。
学物理的人了解了这些像诗一样的方程的意义以后,对它们的美的感受是既直接而又十分复杂的。
它们的极度浓缩性和它们的包罗万象的特点也许可以用布雷克的不朽名句来描述:
一粒砂里有一个世界
一朵花里有一个天堂
把无穷无尽握于手掌
永恒宁非是刹那时光它们的巨大影响也许可以用波普的名句描述:
自然与自然规律为黑暗隐蔽:
上帝说,让牛顿来!一切即臻光明。
可是这些都不够,都不能全面地道出学物理的人面对这些方程的美的感受。缺少的似乎是一种庄严感、一种神圣感、一种初窥宇宙奥秘的畏惧感。我想缺少的恐怕正是筹建哥特式教堂的建筑师们所要歌颂的崇高美、灵魂美、宗教美、最终极的美。
(摘自《文汇报》2001年5月8日)
[1]