首页 -> 2007年第8期
聋生与听力正常学生构建加减文字题问题模型的比较研究
作者:于素红 方俊明
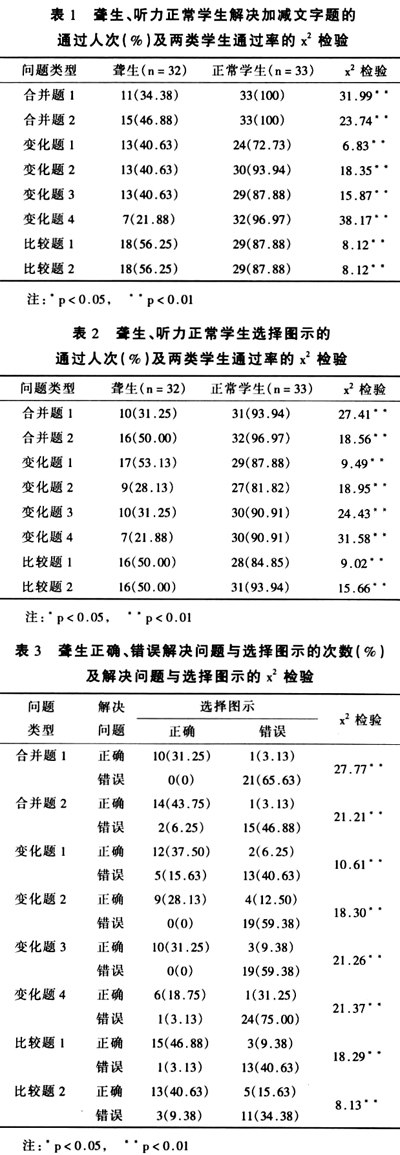
3.3 聋生选择图示与解决加减文字题的关系
聋生选择表达文字题变量关系的图示与解决加减文字题的关系见表3。由表3可知,在每道构建问题模型更有利于问题解决的加减文字题上,聋生解决加减文字题的成绩都与其选择图示的成绩有着极为密切的关系;绝大多数选择图示正确的聋生能够正确地解决文字题,绝大多数选择图示错误的聋生解决文字题也出现错误。
4 讨论
4.1 构建问题模型在聋生解决加减文字题的过程中有着重要的作用
在设计实验时,考虑到问题表征策略等因素可能会影响聋生对文字题的表征,为了更好地探讨问题模型构建与文字题解决的关系,我们在无图示提示解决文字题的实验部分要求被试每解决完一道文字题后都要回答3个问题,这实际上是在提醒被试要关注文字题的文本信息、在正确表征的基础上解决文字题。本研究发现在这样的提示下,聋生解决构建问题模型更有利于问题解决的加减文字题的通过率仍然很低,显著落后于听力正常学生。我们在选择图示的实验部分,每道文字题都提供3个图示供被试选择,这实际上降低了被试独立表征问题、构建问题模型的难度。本研究发现在这样的条件下,聋生在所有文字题上选择图示的通过率都很低,显著落后于听力正常学生。本研究假设能够正确选择表达文字题变量关系的图示说明学生在一定程度上建构了正确的问题模型,因此,我们认为,与同年级的听力正常学生相比,聋生构建加减文字题问题模型的能力是较差的,而聋生解决加减文字题的成绩显著落后于听力正常学生是与其问题模型构建能力差有关的。
本研究还进一步分析了聋生选择图示的成绩与解决加减文字题成绩的关系,结果发现在所有文字题上,聋生解决文字题的成绩都与其选择图示的成绩有着密切的关系,构建正确的问题模型更有利于正确地解决加减文字题,而不能构建正确的问题模型更容易出现解题错误。由此可见,构建问题模型在聋生解决加减文字题的过程中有着重要的作用。
4.2 聋校文字题教学应该重视学生问题模型的建构
在聋校的数学文字题教学中,加减文字题是聋生最早学习的也是相对来说比较简单的文字题。但实践中,聋生在解决加减文字题时仍然存在很多困难,特别是当需要同时解决多种类型的加减文字题时,聋生遇到的困难就更大了。造成这种现象的原因是复杂的。聋生可能在解决文字题的每个阶段中都存在一定的问题,通过本研究可以肯定的是聋生在问题表征阶段构建问题模型的能力差是其中的原因之一。因此,我们建议教师在加减文字题的教学中,要重视培养聋生理解文字题各变量间关系、构建问题模型的意识和能力。而对于语言发展水平相对落后的聋生而言,学会根据文字题的具体图式用画线段图的形式构建文字题的问题模型可能是帮助其理解文字题变量关系的有效方法之一。
5 结论
5.1 聋生解决加减文字题和构建问题模型的成绩都显著落后于听力正常学生。
5.2 构建问题模型在聋生解决加减文字题的过程中有着重要的作用。
5.3 在聋校文字题教学中要重视问题表征训练。
参考文献
1 Kintsch W, Greeno J G. Understanding and solving arithmetic problems. Psychological Review, 1985, 92(1): 109-129
2 Riley M S, Greeno J G. Developmental analysis of understanding language about quantities and of solving problems. Cognition and Instruction, 1988,5(1):49-101
3 Hegarty M, Mayer R E, Monk C A. Comprehension of arithmetic word problems: a comparison of successful and unsuccessful problems solvers. Journal of Educational Psychology, 1995,87(1): 18-32
4 Cardelle-Elawar M. Effects of teaching metacognitive skills to students with low mathematics ability. Teaching and Teacher Education,1992, 8: 109-121
5 Cummins D, Kintsch W, Reisser K, Weimer R. The role of understanding in solving word problems. Cognitive Psychology, 1988, 20, 439-462
6 De Corte E, Verschaffel L, DeWinn L. The influence of rewording verbal problems on children's problem representation and solutions. Journal of Educational Psychology, 1985,77,460-470
7 周新林. 儿童解答加减文字题的基本心理过程.博士论文.北京:中国科学院心理研究所,2002
8 Riley M S, Greeno J G, Heller J I. Development of children's problem-solving ability in arithmetic. In Ginsburg H P(ed.), The Developmeny of Mathematical Thinking Academic Press, New York, 1983,153-196
9 Mayer R E, Hegarty M. The process of understanding mathematics problems. In: Sternberg R J, Talia Ben-Zeev ed. The Nature of Mathematical Thinking. Hillsdale, NJ: Lawrence Erlbaum Associates, 1996, 3-25
10 Okamoto Y. Modeling children's understanding of quantitative relations in texts: a developmental perspective. Cognition and Instruction,1996, 14(4):409-440
11 Quintero, A. H. Conceptual understanding in solving two-step word problems with a ratio.Journal for Research in Mathematics Education, 1983,14: 102-112
12 Cummins D. Children's interpretations of arithmetic word problems. Cognition and Instruction, 1991,8(3):261-289